Differential Equation of Linear S.H.M

At $t=\frac{2T}{3}$ a particle is at $\frac{-A}{2}$ and moving towards mean position. Find the equation of SHM. Also find the speed at $\frac{T}{4}$

A particle performs S.H.M. with amplitude $A$. The speed of particle is doubled at the instant when it is at $\frac{A}{2}$distance from mean position. The new amplitude of the motion is

If initially a particle is at$x=\frac{-A}{\sqrt{2}}$ and its position is given by $x=A\cos \left(\omega t+\varphi \right)$ ) then find $\varphi$ if the particle is moving away from the mean position?

If velocity of body is half the maximum velocity. Then what is the distance from the mean position?

A particle moves on the$x$-axis according to the equation $x=\left(5 + 2 \sin \omega t\right) \mathrm{m}$.The motion is simple harmonic with amplitude

The displacement of a particle executing simple harmonic motion is given by$y=A_0+A\sin \omega t+B\cos \omega t$.Then the amplitude of its oscillation is given by

Describe the motion corresponding to $x-t$equation, $x=10-4\cos \omega t$

Derive an expression for displacement of a particle performing linear simple harmonic motion.

If the maximum velocity of a particle performing S.H.M. is $v$, then the average velocity during its motion from one extreme position to the other will be 

Displacement of a particle is given by $y=0.2\sin \left(10\mathrm{\pi }t+1.5\mathrm{\pi }\right)$. Is it simple harmonic? If so, what is its period?

Two linear simple harmonic motions with same amplitude and frequency $\omega$ and $2\omega$ get superimposed on a particle in $x$ and $y$ direction. If the phase difference between the two are $\frac{\pi }{2}$ initially, the resultant path will be:

The displacement of a particle executing SHM is given by $X=3\sin \left[2\pi t+\frac{\pi }{4}\right]$ where $x$ is in meters and $t$ is in seconds. The amplitude and maximum speed of the particle is

A particle performs linear S.H.M. of period $4$ seconds and amplitude $4\mathrm{cm}$. Find the time taken by it to travel a distance of $1\mathrm{cm}$ from the positive extreme position.

If $y=A\sin \left(kx-\omega t\right)$, then find $\frac{{\displaystyle \frac{dy}{dx}}}{{\displaystyle \frac{dy}{dt}}}$.

Find $\left(v\right)$ and $\left(a\right)$ in following equation of SHM.

 $x=10\sin \left[2\pi t+\frac{\pi }{4}\right]$

A particle performs SHM along $x$-axis. It starts from rest from $x=-1$ at $t=0$ and it reaches with maximum speed at $x=+1$ for $1^{\mathrm{st} }$ time at $t=3 \mathrm{s}$. Calculate time (in sec) when it reaches at $x=+2$ for second time.

Find the time period of following simple harmonic motion:

(i) $y=4\cos 30t$

(ii) $y=10\sin \left(45t+5\right)$

The displacement of two particles executing S.H.M are represented by $y_1=a\sin \omega t$ and $y_2=a\cos \left(\omega t+\varphi \right)$. The phase difference between the velocities of these particles is

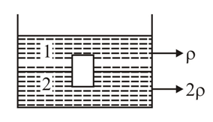
A plank of area of cross-section $A$ and mass $m$ is half immersed in liquid $1$ of density $\mathrm{\rho }$ and half in liquid $2$ of density $2\mathrm{\rho }.$ What is period of oscillation of the plank if it is slightly depressed downwards.

A simple pendulum completes $20$ oscillations in $30 \sec$ and go to a maximum distance of $15 \mathrm{cm}$ from its rest position. If at the start of the motion, the pendulum has angular displacement of $\frac{\mathrm{\pi }}{6}$ rad to the right of its rest position. Write the displacement equation of the pendulum.